Sådan finder du området for en ensartet trekant

Matematik, og især geometri, ifølgemeningsmålinger af skolebørn, en af de mest utrolige lektioner, og alt for at de får dig til at lære et stort antal formler, der i livet 90% af de nuværende voksne ikke har fundet praktisk anvendelse. Men i et øjeblik lærer vi formler, løser problemer, gør ligninger ikke for, at de kan være nyttige for os i livet, men fordi det udvikler tænkning og logik. Selv de gamle græske vismænd sagde, at det menneskelige intellekt kan måles ved viden om matematiske videnskaber. Og siden du besluttede at blive bekendt med anvendelsen af formlerne for en ensartet trekant - vi tager os hånd i hånd og læser hele artiklen.
Før du begynder at besvare spørgsmålet, hvordan du finder detområdet af en ensartet trekant og gå til den praktiske del af artiklen, hvor formler og beregninger er givet, lad os betegne selve konceptet for os selv. En ensartet trekant er en trekant, hvor to af de tre sider er lige i længden, kaldet laterale sider. I tilfælde af en regelmæssig trekant, hvor alle sider er lige, betragtes den også som enslig, men omvendt, når en ensartet trekant anses for korrekt - er falsk.
Triangles sider skal udpeges, vi gør det på denne måde som vist på billedet nedenfor, hvor: a - sider, b-base og h-højde.
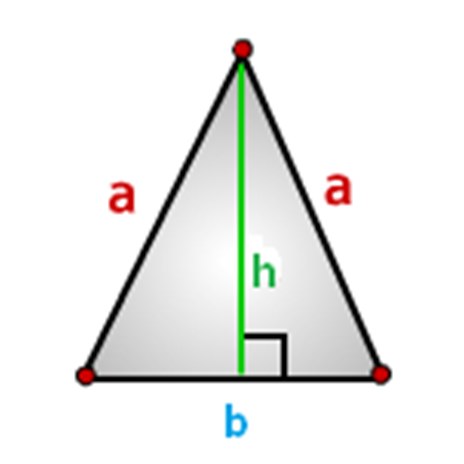
Sådan beregnes området af en enslig trekant, formler.
Når vi har lavet notationen af højde, sider og vinkel, kan vi begynde at løse problemet.
Til at begynde med vil vi bestemme, hvad vi kender.
Hvis højden og bunden - så den klassiske formel (* - multiplikationstegn):
S = ½ * b * h
Lad os erstatte for eksempel tallene hvor: h = 16, b = 18, får vi følgende:
S = ½ * 18 * 16 = 9 * 16 = 144;
Arealet af en ensartet trekant er S = 144 cm2
Der er andre formler, der kan hjælpe osi hvordan man kender området af en enslig trekant. En sådan formel er Herons metode. Lad os ikke skrive en kompleks formel, vi tager forkortet en forkortet:
S = ¼ b √4 * a2-b2
Det er klart, at b er grundlaget, og - lige sider. Formlen er egnet i tilfælde hvor h-højden er ukendt.
Ved at erstatte værdierne, lad a = 6, b = 3, vi får følgende:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Du kan bruge til at beregne området lig med siderne af trekanten og vinklen mellem siderne:
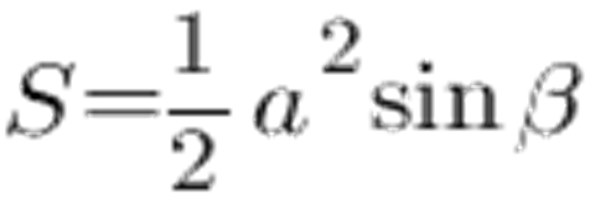
Ifølge sinusbordet er vinklen ved 45 ° lig med 0.7071, siden a og lad den være 6 cm, vi opnår følgende:
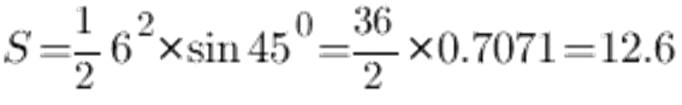
Som følge heraf er arealet af en ensartet trekant 12,6 cm2.
Der er også måder at beregne området på, herunderherunder i tilfælde af en enslig trekant, men de er ret komplicerede og gælder ikke for "elementære" beregninger, som dem der er angivet ovenfor, i begrebet kompleks matematik. Og det er ikke værd at tale om ting, som selv lærere med erfaring ikke forstår.
Så, du kan trække vejrligt suk på dettelille geometri kursus om at finde arealet af en ligebenet trekant, vil blive betragtet som afsluttet, og den opnåede viden som et resultat af at læse artiklen - lektioner på "fem".